|
|
I - CHING e IL COMPUTER
|
|
La numerazione
binaria che oggi usiamo nei calcolatori, non è un sistema di numerazione
inventato da Leibniz. Il grande matematico descrisse un sistema già usato dagli
antichi cinesi, lui cercò solo di capirci qualcosa creando un sistema numerico;
ma nel farlo fu poi quasi deriso; ma in seguito questa
"chineseria" fu ripresa da Boole che ci capì qualcosa di più, ma la sua
grande importanza la si scoprì in tempi recentissimi quando fu usato nei
circuiti degli elaboratori elettrici (a relè) poi nei circuti elettronici dei
computer che stiamo usando in questo momento.
Leibniz fu solo
il primo che lo descrisse questo sistema nello scritto De
Progressione Dyadica, pubblicato nel 1679. Ma c'è un antefatto; Liebniz (fra
l'altro bibliotecario) era in corrispondenza con un gesuita missionario in Cina,
padre Joachim Bouvet, che fece conoscere al grande matematico i curiosi
diagrammi con gli esagrammi riportati in un testo antico molto diffuso in
Cina, quanto la Bibbia in Europa. (quello che ricevette Leibniz, antico, lo
pubblichiamo qui a metà pagina):
"Curiosi - scrisse Bouvet - perchè i
cinesi da questi esagrammi del Libro dei I-CHING (detto anche Oracolo delle
Mutazioni, e le cui origini si perdono nei miti della Cina preistorica -
4000 fa), riflettono le "mutazioni" che avvengono costantemente in tutti i
piani dell'universo, inoltre -affermano i cinesi- è concepito per gettare luce
sul mondo nascosto dietro le apparenze, e agisce quale guida ai misteri dell'io
inconscio. Quindi oltre che un testo con una base scientifica, ha degli
aspetti descrittivi e normativi dell'etica dell'uomo, fornisce indicazioni su
quali criteri e valori devono essere rispettati da chi agisce".
Bouvet diceva
il vero. Infatti, le due maggiori "religioni" cinesi, il
taoismo e il confucianesimo, si ritrovano nelle pagine dell'I-Ching. Lao
Tse fondatore del taoismo poggia molti suoi insegnamenti sulla saggezza
dell'oracolo, e lo stesso Confucio lasciò scritto una serie di commentari
proprio su I-Ching. Curiosa una sua affermazione riportata dagli
Analettici (VII, xvi) "Se potessi aggiungere alcuni anni alla mia vita,
ne dedicherei cinquanta allo studio dei I-Ching, così eviterei di commettere
grandi errori".
Padre Bouvet, un
gesuita curioso, indagatore, matematico e filosofo, in Cina rimase forse
sconcertato nel vedere che il testo dei I-Ching non era preso in
considerazione solo da individui di bassa cultura, come un oracolo pagano, ma
che per filosofi e scienziati il testo era fondamentale, lo usavano da
secoli, e su questo sistema avevano creato non solo alcune correnti di
pensiero ma anche quelle scientifiche. Quindi Bouvet riteneva che da parte
occidentale questo testo per lui quasi impenetrabile richiedesse un maggior
approfondimento "scientifico-matematico" e anche filosofico. E chi meglio di
Leibniz poteva analizzarlo?
Il matematico lo riceve e lo esamina
per giorni e giorni; resta poi fulminato nell'intuire le possibilità
potenziali di questo testo tre volte millenario. Scopre dal grande cerchio dei
64 esagrammi (o dal quadrato al centro con 8 x 8 caselle) che se sostituiva la
linea spezzata con lo 0 e la linea intera con un 1, poteva rappresentare
qualsiasi numero in una progressione "binaria". Non solo, ma forse intuisce
pure, che ogni altro tipo di informazione umana, con lo stesso sistema,
affidandosi ad alcune sequenze numeriche (in binario) ci si poteva costruire
convenzionalmente (tutti gli alfabeti sono segni convenzionali) alcune lettere
di un immaginario "alfabeto", di conseguenza parole, frasi; dunque
anche esprimere dei concetti. Come arrivò a questa conclusione non lo
sappiamo; la corrente, i relè e le valvole termoioniche non
esistevano e l'on-off neppure poteva immaginare cos'era, e altrettanto il
polo positivo e il polo negativo, figuriamoci poi le porte logiche o gli
indirizzi di memoria che (in binario) sono oggi universali.
Ora sappiamo che ne
I-Ching, le linee intere e quelle spezzate hanno lo scopo di rappresentare i
principi fondamentali dell'esistenza.
La linea intera ( ____ ) fu chiamata YANG, e significa il " polo positivo
" (attivo) (lo 0)
La linea spezzata ( __ __
) fu chiamata YIN, esignifica il polo "negativo" (passivo) (
l' 1)
Poi i cinesi per
mostrare i rapporti tra questi due opposti, le due linee furono combinate in
coppia allo scopo di formare il maggiore e il minore Yang e il maggiore e il
minore Yin. Poi venne aggiunta un'altra linea, che formò le otto possibili
figure trilineari o trigrammi. Ad ognuno di questi trigrammi venne dato un nome
e certi attributi di base. Combinando in coppie i trigrammi si giunse a formare
64 figure di sei linee ognuna, dette esagrammi. Poi si nominarono uno per uno
aggiungendo un testo interpretativo. E ogni parte del testo (Sentenza,
Commento) era (e lo è ancora) il responso di due trigrammi
combinati. Nulla fu fatto a caso come vedremo.
Leibniz comunque
senza tanto badare alla simbologia e al testo, ma concentrandosi sui segni, creò
in poche parole con la "sua" logica (ma come vedremo questa era matematicamente
già presente) il suo SISTEMA BINARIO. Ne
parlò in giro con i colleghi, risero in molti, sembrò una speculativa e astratta
bizzarria di un matematico, non ci capirono nulla, e fu alla fine dimenticata.
La riscoprì BOOLE, molto più tardi. Riprendendo gli studi di Leibniz, nel 1855,
ci costruisce la sua logica binaria. Ma anche i suoi risultati sono presi
come una stramberia. Non hanno un impiego pratico.
A parte questi
due estemporanei e autorevoli interessamenti, l'I-Ching come testo
oracolare, rimase in occidente sconosciuto fino al 1882, quando l'irlandese
James Legge, ne fece una traduzione in inglese, molto intricata, ma anche lui,
inutile, perchè non spiegò (ed era la parte più profonda - visto l'uso
filosofico che se ne faceva in Cina) come potevano essere usati gli
esagrammi; anzi lui stesso nel commentarli, con molto scetticismo negò a
I-Ching la funzione di oracolo; si potevano solo soggettivamente
interpretare, e ognuno poteva fare uscire la risposta "che
desiderava". Con queste premesse il libro fece la stessa fine di quelli di
Leibniz e di Boole; fu considerato una bizzarria, questa volta di uno
scrittore, un'altra "Chinoseria".
L'I-Ching li riprese
in mano Gustav Jung. Li utilizzò per un'indagine psicologica, cercando
chissà cosa; ma si arrese subito, pur trovando alcune risposte
nell'oracolo stupefacenti, che gli permettevano una percezione profonda
del problema che lo preoccupava. Nella sua autobiografia,
Ricordi, Jung descrive queste percezioni: "Vi trovo delle
singolari risposte, risultati di ogni genere, connessioni significative, ma
purtroppo nel corso dei miei pensieri io non riesco ancora a spiegarmi molte
cose".
Poi vennero altre pubblicazioni; nel 1929 e una nel 1949.
Quest'ultima, in inglese ebbe più successo, ma più che altro fu una curiosità
per gli amanti del mistero o in cerca di nuove credenze religiose; quindi
un'altra "cineseria". Fra l'altro lo studio era stato fatto sui I-Ching in
quella versione stesa e commentata dal filosofo cinese Sung Shao Yung verso il
1060 d.C.
L'ordine degli esagrammi apparivano sistemati in un modo
diverso da quello antico, e cosa strana e singolare, nessun altro estensore o
commentatore nei successivi secoli accennò minimamente che l'oracolo
avesse una relazione col mondo dei numeri; cioè con la matematica, simile
a quella della scuola pitagorica (ancora oggi discutibile - leggi Geymonat,
Storia del pensiero filosofico e scientifico. Capitolo, "I numeri principio
della realtà") che in quanto a originalità c'era molto poco. Certamente la
dimostrazione riferita negli Elementi di Euclide non fu fatta da
Pitagora; ma anche in quella che era uscita dalla sua Scuola non vi era
molta chiarezza sulla "discontinuità", c'era il più astruso "labirinto" della
ragione. Infatti, il rapporto tra continuo e discontinuo resterà, per tutta la
storia del pensiero umano, un problema molto difficile e molto dibattuto. I
pitagorici non s'inoltrarono nel "labirinto", e i successivi scienziati non
trovarono altra via se non quella di scindere completamente la geometria
dall'aritmetica, interpretando la prima come studio del continuo e la seconda
come studio del discontinuo. La svolta che poi avvenne con il cristianesimo
bloccò definitivamente questa speculazione.
Ma torniamo a
Padre Bouvet. A Leibniz il gesuita inviò non una tavola degli
esagrammi posteriori all'anno 1060, ma una antecedente (che pubblichiamo qui)
dal prete chissà dove scovata, e Leibniz, chissà come, ci costruì il
suo sistema binario, che si basa sulla permutazione di due cifre o quantità. E
visto che poi non fu di nessuna utilità pratica, non si capisce perchè perse
tanto tempo per nulla. Ma qualcosa Leibniz cercava! La sua irriducibile e
ostinata lotta (implacabile sulle sue Epistole) sul dualismo
cartesiano era appena iniziata. Dunque un motivo c'era. E si affannava a darsi
una risposta che non veniva.
Mai più pensava Leibniz di avere scoperto (o
riscoperto) con il suo sistema la più importante convenzione oggi adottata dai
computer che è basata su un "naturale" stato o principio: proprio quello della
dualità. Quasi una beffa del destino!
Infatti questo
"lavoro" di Leibniz non solo anticipava di un secolo e mezzo la "logica"
di G. Boole, ma anticipava quello che sarebbe stato poi il vero linguaggio
del calcolatore, con il quale il programmatore fornisce istruzioni allo
stesso e il linguaggio in base al quale esso interpreta, senza sapere che cosa
significhino, le istruzioni che riceve, ed elabora in termini puramente binari
ogni informazione di tipo classico opportunamente introdotte sempre in binario
(o tramite un linguaggio che usando stringhe di bit crea parole
(convenzionali) di istruzioni o comandi molto più semplici)
Dunque
quello di Leibniz era un sistema posizionale che usava due soli simboli (
0 e 1 ) operando in base 2; un qualsiasi numero è cioè rappresentabile mediante
una serie di zeri e di unità, che devono essere moltiplicate per una potenza di
2 a seconda della posizione occupata e poi sommate fra loro. Per esempio il
numero binario 101101 si deve interpretare come
1 X 25 + 0 X 24 + 1 X 23 + 1 X 22 + 0 X 21 + 1 X 20
( un esacalcolo (!!!) o un esagramma? )
e corrisponde al
numero 45; nel caso di numeri con la virgola si usano le potenze negative di
2.
(più avanti spiegheremo come si fa)
Questa numerazione
binaria si rivelò in seguito utilissima negli elaboratori (elettromeccanici poi
elettronici) perchè usano (due sole cifre. Per esempio un circuito elettrico può
essere aperto o chiuso e i due possibili stati si possono far
corrispondere all'unità e allo zero; una serie di circuiti può servire perciò a
rappresentare qualsiasi numero. Inoltre in logica matematica, una preposizione
può essere soltanto vera o falsa e le due possibilità sono simbolizzate mediante
le cifre 1 e 0: e l'algebra di Boole, impiegata poi negli elaboratori, si fonda
su questo presupposto.
Boole (e sembra molto singolare anche questo)
enunciando la sua "logica booleana" non intitola la sua opera con un termine
matematico, lui che è un puro matematico, ma gli dà un nome quasi filosofico:
"Investigazione sulle leggi del pensiero". Probabilmente chi acquistò il
libro attirato dal titolo rimase molto deluso nel trovarsi poi dentro in questo
enigmatico testo, e forse si chiese a cosa serviva e perchè quel titolo, visto
che parlava di numeri. E in effetti era un'altra "Chinoseria"
incomprensibile
LEIBNIZ aveva quindi creato il suo Sistema
Binario, BOOLE molto più tardi riprendendo gli studi di
Leibniz aveva costruito la sua logica binaria, poi ZOSE
(nel 1936) ATANASOFF (nel 1939) (uno con i relè, l'altro con le
valvole termoioniche) e NEUMANN (nel 1945-46) l'hanno
usata per elaborare il linguaggio macchina del computer, con
i commutatori elettrici poi elettronici (chiamati circuiti flip-flop) che
hanno due posizioni. Uno inserisce la corrente, l'altro la disinserisce. Queste
due posizioni sono rappresentate dal numero 1 e dallo 0. - 1 per inserire, e 0
per disinserire.
(l'attivo e il passivo YANG e YIN)
MA ADESSO
VIENE IL BELLO !!!!!!!
Intanto analizziamo il curioso termine
suan, che in cinese esprime calcolo
ma
suan significa in cinese anche rivelazione divina
E
in Cina il rapporto tra matematica e divinazione é stato sempre stretto.
L'universo fu suddiviso nei principi opposti ma complementari di Cielo e Terra
(e qui ritorna Yang e Yin). Il Cielo che abbraccia la
Terra fu indicato con il numero 1, la terra con il numero 2. Il Cielo principio
attivo, la Terra principio passivo.
Ma il numero 1 era speciale,
non doveva essere il primo di una serie che continuava all'infinito, ma doveva
rappresentare il simbolo del cuore dell'universo intero. Ed era così
astratto nel processo dei mutamenti che non fu coinvolto perchè rappresentava la
totalità dell'esistenza. Fu deciso così di non usarlo. Alla Terra rimase
il 2, e al Cielo fu assegnato il 3.
L'Universo (1 apparente) fu diviso
nei principi opposti ma complementari, PARTENDO quindi DAL 2
Tutti i numeri
pari furono assegnati alla Terra, mentre tutti i dispari a partire dal 3
assegnati al Cielo. (Yin e Yang)
Il binario (o meglio quello di Leibniz
del 1679) si basa sulla permutazione di due cifre o quantità nel suo
sistema.
Ed è identico a l'I-Cing (concepito 3700 anni
prima di Leibniz)
Affermare che sia stato il caso sarebbe pura follia. E
lo vedremo più avanti.
Un circuito in serie di commutatori elettronici
odierni, può formare un numero nella progressione binaria....o...
un
esagramma dei I-CHING. (lo vedremo presto qui
sotto)
Incredibile ma vero! Dobbiamo quindi documentarla questa
operazione ripartendo dall'aritmetica che abitualmente usiamo, che ha come
base il 10. (non dimentichiamo che lo 0 (usato da Fibonacci nel 1200) fu
introdotto in occidente dagli arabi che a loro volta lo avevano mutuato
dagli indiani, ed è legato allo sviluppo di un sistema numerico decimale
posizionale, che i greci ignoravano)
Aggiungendo uno zero a ogni numero
lo moltiplichiamo per 10. Leibniz ai suoi tempi questo lo sapeva già, ma fu il
primo a realizzare la possibilità di un'aritmetica che avesse (e qui ripete
quello che hanno fatto i cinesi) come base il 2. Infatti, la progressione per 2,
che viene chiamata progressione binaria o diadica, moltiplica ogni numero solo
per due quando uno zero viene aggiunto. (notare il 2 il 4 e l'8)
Per
esempio, i primi dieci numeri della nostra normale progressione nella
progressione binaria diventerebbero
1 = 1
2 =
10
3 = 11
4 = 100
5 = 101
6 = 110
7 = 111
8 = 1000
9 =
1001
10 = 1010
Andiamo ora sugli esagrammi, a scoprire lo stupefacente!
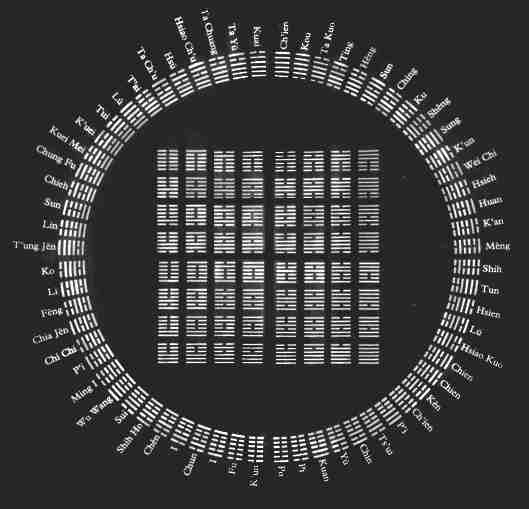
Partiamo dal basso, dall'esagramma Po (in fondo, in mezzo al cerchio, il secondo a sinistra in senso antiorario) che è 1 nella progressione binaria se si ignorano gli zeri che precedono; ma anche qui l'esagramma subito a sinistra di Po, il K'un, è composto da sei line spezzate, cioè 000000) Il successivo esagramma, Pi, a destra di Po, è 2 (espresso come 10 nella progressione binaria), e così di seguito.
Per fare un controllo, il modo migliore è di iniziare con un numero nella nostra progressione abituale di 10, quindi trasformarlo nella progressione diadica. (quello che abitualmente fanno tutti i programmatori con il "linguaggio macchina")
Per fare questo
occorre dividere il numero per 2, scrivere il quoziente sotto e il resto di
fianco. Poi dividere ancora il quoziente per 2, mettere il nuovo quoziente sotto
e il resto di fianco; quindi continuare in questo modo fino a quando si ottiene
un quoziente uguale a zero. La colonna laterale dei resti è il numero da cui
siamo partiti espresso nella progressione binaria.
Ora per
trasformarlo in esagramma, tracciamo una linea spezzata accanto ad ogni 0 e una
linea intera accanto ad ogni 1. Questo ci darà l'esagramma che corrisponde al
numero col quale abbiamo iniziato.
2 esempi: il
risultato in fondo a queste due tabelle è utile
per ricavare da un
numero qualsiasi 1 o 0
mentre quelli a destra forniti dai
resti danno sia il numero binario e nello stesso tempo la linea intera o
spezzata dei 64 esagrammi dei I-Ching.
|
es. n. 50 diviso 2 ..............=
25 resto 0 = ___ ___ diviso 2
= 0 |
es. n. 64 diviso
2
.............= 32 resto 0 =
___ ___ diviso 2 =
1 |
|
se il risultato ci fornisce meno di 6 righe per formare l'esagramma si aggiungono tanti zeri per completarlo. | |
l' on-off =
acceso-spento, inserito-disinserito, polo positivo-negativo lo otteniamo alla
base.
cioè lo Yang e Yin = attivo-passivo, polo positivo-negativo,
maschio-femmina.
Senza dover
illustrare tutti i vari simbolismi "filosofici" oppure "oracolari" dei I-Ching,
cerchiamo di restare legati al pensiero fondamentale della dottrina pitagorica:
"I numeri sono il principio di tutte le cose. Tutte le cose che si conoscono
hanno un numero; senza questo nulla sarebbe possibile pensare, nè
conoscere".- Alla scuola di Pitagora era apparso inadeguato il principio
unico dei naturalisti ionici. Per rendere conto di questi più complessi problemi
sdoppiarono il principio in due opposti: da una parte il principio del limitato,
del finito, dell'unitario, che rappresentava l'ordine, il cosmo, il bene;
dall'altra il principio dell'illimitato, dell'infinito, che raffigurava il
disordine, il caos, il male. La loro grande intuizione (almeno così ci è stata
tramandata) consistette nel vedere nei numeri e nei loro rapporti "la
chiave" e la struttura ultima di questo assetto dualistico della realtà. Ma col
termine "numeri" i pitagorici intendevano soltanto i numeri interi, concepiti
come collezioni di più unità. Non fecero (!?) particolari indagini sulla natura
di queste unità, limitandosi a rappresentarle con punti, circondati ciascuno da
uno spazio vuoto. Volevano ad ogni costo cogliere il modo con cui dalla
collezione di più unità si generano tutti gli esseri. Le leggi della formazione
dei numeri venivano considerate come leggi della formazione delle cose, e si
riteneva di poter trovare in esse la vera ragione esplicativa del mondo
fisico e morale.
La più importante di queste leggi era costituita
dall'opposta struttura dei numeri dispari e di quelli pari. L'antitesi
dispari-pari veniva così assunta a principio di una serie di altre nove
opposizioni, che spezzavano il mondo in due: limitato-illimitato, uno-molti,
maschio-femmina, luce-tenebre, acceso-spento, buono-cattivo,
quadrato-rettangolo, attivo-passivo, cielo-terra, ecc.
Alcune di queste
nove opposizioni avevano palesemente un carattere fisico; altre invece un
preciso carattere morale. Quindi questa presenza di significati multipli finiva
con l'infondere ai numeri in generale, e a certuni di essi in particolare, un
vero e proprio valore magico-simbolico.. Così un certo numero
dispari veniva assunto per rappresentare una cosa, quello pari fu legato a
un'altra..
Prendiamo ora i primi fondamentali dieci esagrammi
cinesi e ricordiamoci della suddivisione CIELO (tutti numeri dispari), TERRA
(tutti numeri pari) e seguiamo le relazioni date dai creatori dei I-Ching.
(ma anche qui non dimentichiamo il valore magico-simbolico,
che ci ricorda moltissimo quello pitagorico)
Intanto osserviamo
il cerchio che contiene gli esagrammi; è diviso in due, mentre al centro
sono riportati gli stessi esagrammi allineati nella esatta progressione.
Ma partiamo dal cerchio;
In basso, primo a
sinistra, l'esagramma 2 (K'un) ha il il significato di
passività, sottomissione all'1 che ha creato tutte le cose; e non a caso
é rappresentato da sei line spezzate, cioè in binario 0-0-0-0-0-0
(!!!)
In alto, primo a destra, troviamo l'esagramma 1 (Ch'ien)
con il significato cielo attivo, creatività primaria, la fonte di
tutte le cose; e non a caso è rappresentato interamente con sei linee,
cioè in binario 1-1-1-1-1-1 (!!!)
Se invece gli
esagrammi vogliamo rintracciarli nel quadrato 8 x 8 (posto al centro del
cerchio) la ricerca è facilitata, il primo (000000 - 6 righe spezzate) si trova
nell' ULTIMA casella in fondo a destra (la 64), l'altro (111111 - 6 righe
intere) nella PRIMA casella (1) a sinistra in alto.
Attenzione, abbiamo
finora parlato della tabella sopra, cioè quella dei I-Ching
MENTRE QUESTA SOTTO
E' LA RAPPRESENTAZIONE DELLA MEMORIA
DI UN COMPUTER CON I SUOI
INDIRIZZI
ENTRAMBE LE DUE TABELLE COINCIDONO IN REALTA'
ALLA
RAPPRESENTAZIONE BINARIA. E SONO PERFETTAMENTE
IDENTICHE !!!
|
000000 |
000001 | 000010 | 000011 | 000100 | 000101 | 000110 | 000111 |
| 001000 | 001001 | 001010 | 001011 | 001100 | 001101 | 001110 | 001111 |
| 010000 | 010001 | 010010 | 010011 | 010100 | 010101 | 010110 | 010111 |
| 011000 | 011001 | 011010 | 011011 | 011100 | 011101 | 011110 | 011111 |
| 100000 | 100001 | 100010 | 100011 | 100100 | 100101 | 100110 | 100111 |
| 101000 | 101001 | 101010 | 101011 | 101100 | 101101 | 101110 | 101111 |
| 110000 | 110001 | 110010 | 110011 | 110100 | 110101 | 110011 | 110111 |
| 111000 | 111001 | 111010 | 111011 | 111100 | 111101 | 111110 | 111111 |
INIZIANO E TERMINANO ALLO STESSO
MODO (anche se all'inverso)
SONO 64 CASELLE MA ENTRAMBE PARTONO DALLO 0
E TERMINANO AL 63
(e quest'ultimo è l'indirizzo più grande delle posizioni di
memoria in binario del computer)
I due esagrammi, nei
I-Ching, che abbiamo citato sopra, e così tutti gli altri (a parte la
simbologia) hanno sempre lo stretto legame (in binario) con la suddivisione pari
e dispari, cioè Cielo e Terra e procedono in progressione come nella tabella
sopra..
Nella simbologia legata al numero invece abbiamo: (prendiamo i
primi dieci)
1 (dispari)
Cielo, produce acqua e 6 il numero (pari) della Terra lo completa
2
(pari) Terra, produce il Fuoco e 7 il numero (dispari) del Cielo lo
completa
3 (dispari) Cielo, produce il Legno e 8 il numero (pari) della Terra
lo completa
4 (pari) Terra, produce Metalli e 9 il numero (dispari) della
Terra lo completa
5 (dispari) Cielo, produce Suolo e 10 il numero (pari)
della Terra lo completa
E' una teoria simbolica affidata ai numeri, simile a quella dei Pitagorici, come ci fu riferita da Diogene Laerzio: "i quattro elementi della filosofia greca, sono Fuoco, Acqua, Terra e Aria, e derivano indirettamente dai numeri" (Diogene Laerzio, Vite, Libro VIII, cap.19)
Ci fermiano per il
momento qui. Sembra proprio che oltre a Leibniz, ad entrare in possesso di una
copia del vecchio diagramma, che mostra gli esagrammi in circolo e in quadrato e
che lo stesso Leibniz poi ci ricava (quello che già esisteva - il sistema
binario) ne siano venuti in possesso anche i pitagorici, ma anche loro
come Leibniz ci capirono poco. Ma quest'ultimo (e lo abbiamo dimostrato già
sopra) scoprì in quei segni una cosa molto semplice (e fu geniale
nell'intuirla); che se sostituiva a ogni riga spezzata lo 0, e a ogni
linea intera l'1, i 64 esagrammi procedevano in "progressione binaria" dal
numero 0 al 63, e che si basavano sulla permutazione di due cifre o
quantità.
Oggi i commutatori elettronici (seguendo la tabella sopra
riportata che è la stessa dei I-CHING) operano con lo stesso sistema, flip-flop,
acceso-spento, con i commutatori che hanno due posizioni e sono rappresentate
dal numero 1 e dallo 0. (e con questa informazione procedono su una stringa
(byte) di 64 bit. ( !!!!!! )
Quello che oggi poi appare stupefacente, recentemente scoperto dai neuroscienziati, è che i neuroni nel sistema nervoso centrale degli esseri umani e di altri animali superiori, obbediscono alle stesse leggi. I bottoni sinaptici nel ricevimento degli stimoli (delle informazioni dei cinque sensi) sono "inseriti" o "disinseriti", per effetto della differenza del potenziale elettrochimico ionico delle rispettive membrane (la cui potenza va da -30 mV a +70 mV e determinano l'apertura-chiusura delle stesse membrane). Ioni che a loro volta generano un flusso di corrente negli assoni in pacchetti di quanti, che vanno poi a depositarsi nei neuroni lasciandovi (immagazzinandovi) una traccia; è la "traccia mnestica" (presunta registrazione fisica - "in bit", "in quanti di energia") dei nostri ricordi o esperienze; una traccia che nessuno fino a oggi ha mai visto, ma in cui molte persone credono. I neuroscienziati che la cercano, gli hanno già dato un nome "ENGRAMMMA". ( !!! )
John von Neumann, lo scienziato teorico dell'informazione ha già stimato che i ricordi memorizzati durante una vita umana media dovrebbero ammontare a 2,8-1020 (280.000.000.000.000.000.000) bit; fra quelli che ricordiamo e quelli che abbiamo immagazzinato ma non abbiamo più richiamato alla nostra mente. Ma ci sono! Questo già lo sappiamo con la PET (Tomografia a Emissione di Positroni).
In sostanza
l'engramma dovrebbe comportarsi in questo modo; ad ogni ricezione di pacchetti
di quanti, lascia una traccia dentro nelle nostre "scatolette"(neuroni). Si
comporta come il classico "codice a barre" che il commesso di un supermercato
applica su una scatola di pelati quando questi entrano nelle varie "aree"
dei "magazzini"; un generatore di impulsi elettronici, in pacchetti di
quanti, scrive una traccia ("elettro-mnestica" stampata su un'etichetta o
magnetizzata su un supporto), ed ogni qualvolta la commessa al banco deve
leggere prezzo, caratteristiche o altro, usa all'inverso un lettore che legge la
"traccia di quanti", "memorizzata". (ogni memoria é inserita in molte
connessioni, e ciascuna connessione è implicata in varie memorie - e la nostra
rete neurale è fatta proprio così, comprese le "aree" dei
"magazzini")
Forse l'era dei calcolatori elettronici, e in parallelo la
neuroscienza, potrebbe paradossalmente fornirci una maggiore comprensione
dell'antico Oracolo delle Mutazioni; l' I Ching. O il perchè? di tutte queste
singolari ma anche misteriose corrispondenze con i pitagorici, con Leibniz,
con Boole, e oggi con i nostri calcolatori, e con gli indirizzi del nostro
computer che in questo preciso istante stiamo usando proprio grazie ai l'
I-CHING.
O forse fra poco tutta la logica tradizionale salterà; quella
dei i Ching, la pitagorica (monca), quella di Leibniz , di Boole e di
Neuman (copiata dalla prima), e si ripartirà dallo ZERO. Ora quasi ci
siamo!
Compreso Einstein. La sua equazione sembra sia stata "copiata" a
un autodidatta di matematica; De Pretto, che nel 1903 il 23 novembre, pubblicò
al Reale Istituto Veneto delle Scienze il suo studio; Ipotesi dell'etere
nella vita dell'Universo". Formulava già l'equazione E=mc2. Un anno dopo
Einstein pubblicò il suo lavoro, L'inerzia di un corpo è dipendente dal suo
contenuto di energia?. Non accenna a De Pretto, per Einstein la
riflessione scientifica era fuorviante se si incentrava la questione sull'etere.
(Simile a quell'uno dei cinesi? Quasi una religiosa ortodossia). (1)
Il numero citato
sopra di bit, sembra impossibile raggiungerlo con i nostri chip o una
serie di chip. Ma solo quelli attuali, fatti con il silicio, non quelle nuove
macchine che "sono già allo studio, basate su strutture molecolari
che possono essere specificate da molecole di Dna e quindi realizzare macchine
che sono riproducibili biologicamente. Da questa tecnologia del futuro potrebbe
anche emergere una nuova microelettronica basata sulle proprietà quantiche di
molecole organiche, anzichè utilizzare le proprietà fisiche del silicio che sono
attualmente applicate nel chip. Quello più complesso ha già, su una
"scheggia", circa 25 milioni di transistor; si pensa di arrivare nei
prossimi decenni a 100 mila miliardi di transistori su un centimetro cubo. Ma la
velocità di elaborazione non dipenderà tanto dal numero dei transistori ma dalla
complessità delle interconnessioni tra di essi (come le reti neurali). Si
arriverà dunque, al limite fisico critico delle possibilità offerte dal silicio?
Nessuna paura, a sostituirlo ci penserà il Computer quantico. In grado di
avvicinarsi a quel numero espresso da Neuman. Capace di memorizzare tutte le
informazioni dell'intera nostra vita, fin dalla nascita, minuto per minuto, da
rivedere -con un "lettore quantico"- in ogni momento, come in un film,
addirittura in tridimensionale".
"Esistono già alcuni centri di ricerca
nel mondo che stanno esplorando i possibili metodi di estrazione di energia dal
vuoto quantico, cioè, creare energia letteralmente dal nulla." (Federico
Faggin; inventore del primo microprocessore, relazione tenuta a Vicenza, il 5
ottobre scorso (1999).
"E' già dimostrato che è possibile creare un computer che opera su "qubits": bit di informazione che sono simultaneamente sia UNO che ZERO - un paradosso nella logica tradizionale (in questo caso sia occidentale che orientale. Ndr). Possibile soltanto usando porte logiche quantiche". (cit.Idem)
Ritorneremo dunque al
mondo UNITARIO?
Ma siamo sicuri che la matematica binaria sia davvero
matematica?
Quell'UNO omesso dai cinesi cosa voleva dire?
Un certo Ikuko
Nishimura, che mi scrive firmandosi sempre "Zen" (di italiani non ne ho mai
visti!) afferma che la risposta sta nella geometria non-euclidea di Riemann, Lobaceski, Poincarè
. Sostiene che é un punto essenziale per spronare al dubbio chiunque
s'improvvisi determinista in un universo senza fine.
La risposta ai
posteri! O a Zen. Che speriamo ci "illumini" , anche se farebbe uno strappo alla
regola, perchè la dottrina Zen, afferma che "la verità si trasmette al di fuori
delle scritture" (speriamo che la e-mail non la consideri una
scrittura)
By
Francomputer
Consultati i seguenti testi: (piuttosto frammentari,
mentre io credo di aver fornito
una esposizione facilmente e
sorprendentemente comprensibile a tutti. Il guaio
maggiore è che i filosofi
capiscono poco di computer, e i programmatori poco di filosofia)
Fung Yu-lan, Storia
della filosofia cinese
Geymonat, Storia del pensiero filosofico e
scientifico
Judit Hooper, Dick Teresi, L'universo della mente.
G.M.
Edelman. Sulla materia della mente
John Eccles, La conoscenza del
cervello
McCarthy/Warrington, Neuropsicologia cognitiva
John Barrow, Il
mondo dentro il mondo
Karl Lashley, La fisica della mente
Geoff Dromey,
Algoritmi fondamentali nella programmazione
G.L. Simons, Intelligenza
artificiale, nuova frontiera.
Federico Faggin, "I prossimi
cinquant'anni: sarà l'era del computer quantico?".
(relazione
all'Accademia Olimpica a Vicenza - 6 ottobre 1999)
Alfred Douglas. I
Ching
Sam Reifler. I Ching
R. Wilhelm, I Ching. Prefaz. di
C.G.Jung
John Blofeld, I Ching
(1) Umberto Bartocci,
"Einstein e De Pretto, La vera storia della formula più famosa del
mondo"
Edizione Andromeda, di prossima pubblicazione